Entradas en "canvas"
Pathfinding: A*
Introducción
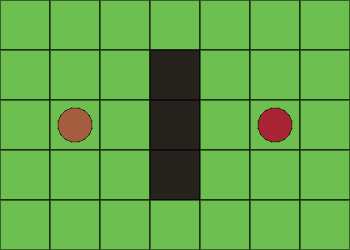
La búsqueda de caminos (pathfinding) es uno de mis problemas favoritos de todos los tiempos y una de las cosas que más he disfrutado programando; por un montón de razones… La primera, es que los humanos creemos erróneamente que es algo que hacemos muy bien, y sólo cuando nos comparamos con una máquina tomamos consciencia de cómo únicamente logramos buenos resultados en entorno sencillos. Por ejemplo, en la imagen siguiente, si estamos en la casilla del círculo marrón y tenemos que ir a la casilla del círculo rojo; y las casillas grises representan un muro, ninguno tenemos problema en esquivar el muro y trazar el camino más corto hacia nuestro destino: la casilla del círculo rojo.
Sin embargo, en la vida real, al conducir o pasear por la calle, no calculamos los caminos entre origen y destino de forma tan matemática como pensamos, y nos dejamos llevar por las anchuras de las avenidas, otros caminos que ya conocemos, la cantidad de luz de una calle, etc. El resultado es que nosotros siempre nos sentimos 100% satisfechos con el camino que hemos elegido, pero muy rara vez este camino es el óptimo; ni el más corto, ni el más rápido.
Me gusta además su enorme utilidad, tendremos que diseñar una solución al problema en cualquier entorno con agentes inteligentes, sistemas robóticos, videojuegos, etc. Y, además, a pesar de su enunciado sencillo, rara vez a los programadores que se enfrentan al problema por primera vez se les ocurre alguna solución que no esté basada en backtracking.
La solución “universal” que durante muchos años ha servido de guía a este problema es el algoritmo A-Estrella (escrito A*). Un algoritmo muy sencillo que ofrece buenos resultados, y ha estado presente en casi todas las aplicaciones de búsqueda de caminos desde el principio de los tiempos hasta la última década.
Vamos a describir en qué consiste y luego lo implementaremos en Javascript.
Desglose y trazas: A*
El problema inicial, como hemos visto, trata de trazar el camino para ir del punto A (círculo marrón) al punto B (círculo rojo).

Idea general:
La primera operación a realizar, es dividir el espacio en casillas. En nuestro ejemplo las casillas son cuadradas, pero realmente podremos adaptar el algoritmo a dividir el espacio de la forma que deseemos (triángulos, hexágonos, etc). A partir de ahora cada casilla será una celda espacial (crearemos una estructura de datos que la represente) relacionada con sus adyacentes y con su “padre”; el padre será la celda por la cual hemos llegado a tener en cuenta a la actual como posible candidata a formar parte del camino final.
Aspectos:
1) Tener dos listas de celdas; una abierta y una cerrada. En la lista abierta iremos introduciendo celdas que tenemos que evaluar, para ver si son buenas candidatas a formar parte del camino final. En la lista cerrada introduciremos las celdas ya evaluadas.
2) La evaluación de las celdas se hace en base a dos factores: la longitud del camino más corto para llegar desde el punto de origen a la celda actual, y la estimación del camino más corto que podría quedar para llegar al destino. La estimación para el destino se hace usando una función heurística, en concreto se suele usar la Distancia Manhattan, que esencialmente consiste en contar cuantas celdas nos separan del destino vertical y horizontalmente, sin movimientos diagonales; como si estuviéramos recorriendo manzanas en una gran ciudad y no pudiéramos atravesarlas, sólo bordearlas; de ahí viene el nombre.
Algoritmo
Paso 0 Añadimos la celda origen a la lista abierta.
Paso 1 Cogemos el primer elemento de la lista abierta y lo sacamos y lo insertamos en la lista cerrada.
Paso 2 Cogemos las celdas adyacentes a la celda extraída.
Paso 3 Para cada celda adyacente:
A) Si la celda es la celda destino, hemos terminado. Recorremos inversamente la cadena de padres hasta llegar al origen para obtener el camino.
B) Si la celda representa un muro o terreno infranqueable; la ignoramos.
C) Si la celda ya está en la lista cerrada, la ignoramos.
D) Si la celda ya está en la lista abierta, comprobamos si su nueva G (lo veremos más adelante) es mejor que la actual, en cuyo caso recalculamos factores (lo veremos más adelante) y ponemos como padre de la celda a la celda extraída. En caso de que no sea mejor, la ignoramos.
E) Para el resto de celdas adyacentes, les establecemos como padre la celda extraída y recalculamos factores. Después las añadimos a la lista abierta.
Paso 4 Ordenamos la lista abierta. La lista abierta es una lista ordenada de forma ascendente en función del factor F de las celdas.
Paso 5 Volver al paso 1.
Factores
Cada celda va a tener 3 factores. G, H y F.
– G: Es el coste de ir desde la celda origen a la celda actual. Cada vez que nos movamos un paso en horizontal o vertical, añadiremos 10 puntos de coste. Cada vez que nos movamos en diagonal, añadiremos 14. ¿Por qué 14? Porque aunque geométricamente la proporción exacta debería ser 14.14213 {sqrt(10*10+10*10)}, 14 es una buena aproximación entera que nos hará ganar velocidad al evitar el uso de coma flotante (nota: en javascript en realidad esta mejora no se aplica, ya que todos los números se tratan como floats internamente).
– H: Es la distancia mínima y optimista, sin usar diagonales, que queda hasta el destino. La heurística basada en Distancia Manhattan de la que hemos hablado antes.
– F: Es la suma de G y H.
Traza explicada
Iteración 1
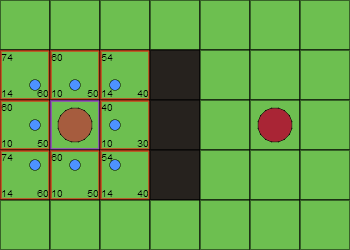
Tras la primera iteración, la celda origen queda en la lista cerrada (border violeta). Las adyacentes quedan en la lista abierta (borde rojo). Las celdas tienen sus tres valores G, H y F calculados. La F aparece en la esquina superior izquierda de cada celda. La G en la inferior izquierda. La F en la inferior derecha.
Además cada celda tiene una bolita azul que indica qué celda es su padre, tras esta iteración, todas las celdas de la lista abierta tienen como padre a la celda origen.
Iteración 2
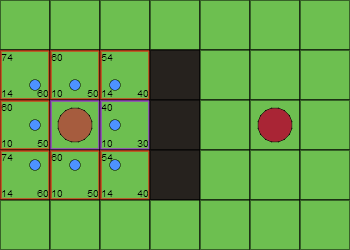
En esta iteración hemos añadido la celda a la derecha (la de menor F de la lista abierta) de la celda origen a la lista cerrada (borde violeta). No se han producido más cambios.
Iteración 3
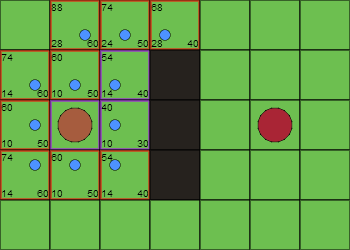
Se añade la celda superior derecha desde el origen a la lista cerrada (es la de menor F de la lista abierta) y se añaden las adyacentes que no estaban ya.
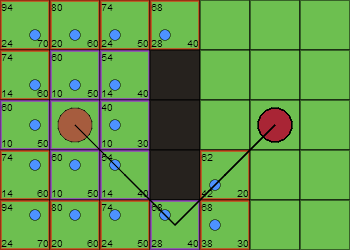
Iteración N
Y algoritmo sigue. De forma sencilla, hasta alcanzar el objetivo:
Ejecución de traza interactiva I
Podéis ejecutar el algoritmo paso a paso haciendo clic en la imagen inicial siguiente. Cada clic equivale a una iteración:
Ejecución de traza interactiva II
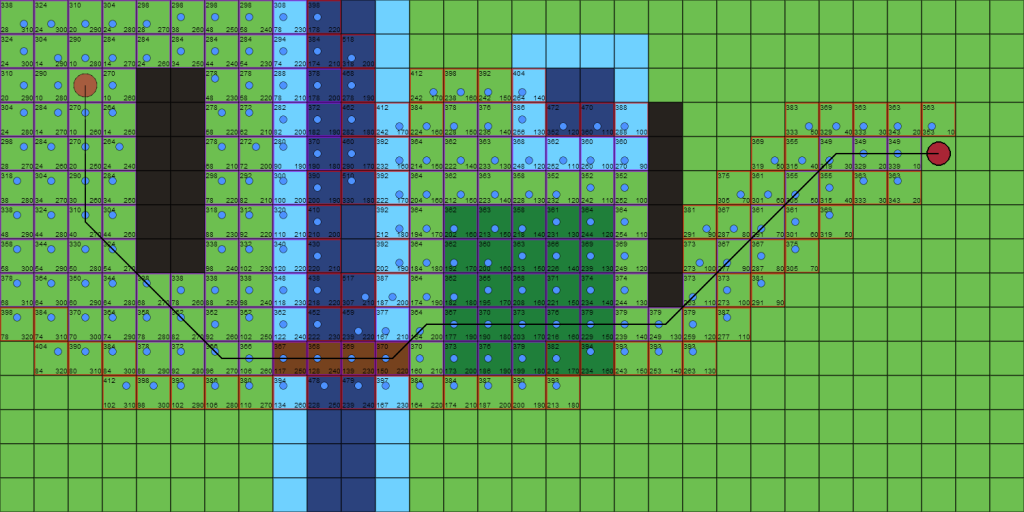
Vamos a darle más juego al algoritmo. Podemos añadir fácilmente tipos de terrenos con diferentes costes a la hora de transitarlos. En el siguiente ejemplo vamos a usar los siguientes tipos de terreno:
– Césped (verde claro): Movimiento al 100%
– Bosque (verde oscuro): Movimiento al 75% de la velocidad normal
– Agua (azul claro): Movimiento al 50% de la velocidad normal
– Agua profunda (azul oscuro): Movimiento al 10% de la velocidad normal
– Muro (gris): Infranqueable (0% de velocidad)
– Puente de madera (marrón): Movimiento al 90% de la velocidad normal
El escenario es el siguiente:
Y el resultado (clic en la imagen para ampliar):
Podéis ejecutarlo paso a paso en la siguiente simulación (tened en cuenta que habrá interacciones vacías que sólo eliminan nodos). Cada clic en el mapa será una iteración.
Y por último… lo más importante; el código 😉
Como siempre, si tenéis cualquier duda, preguntadme 🙂
Os recomiendo leerlo despacio y entenderlo (es muy sencillo y claro). Se lee bien.
function Map(width, height, cell_size, canvas)
{
//-- init
this.width=width || 10;
this.height=height || 10;
this.cell_size=cell_size || 50;
canvas.width=this.width*this.cell_size;
canvas.height=this.height*this.cell_size;
this.ctx=canvas.getContext("2d");
this.origin=0x0;
this.destiny=0x0;
//-- inside globals
var map=this;
var ctx=this.ctx;
//-- members
this.cells=[];
var terrains=[
{awkwardness:1.00, color:"#6DBF50", name:"ground"},
{awkwardness:0.75, color:"#1F7F3A", name:"forest"},
{awkwardness:0.50, color:"#6FD1FF", name:"water"},
{awkwardness:0.10, color:"#2B427D", name:"deep_water"},
{awkwardness:0.00, color:"#26221E", name:"wall"},
{awkwardness:0.90, color:"#76421E", name:"bridge"}
];
// -- allow external access by name (like map.terrain.water...)
(function indexTerrains()
{
map.terrains={};
for(var i=0;i<terrains.length;i++)
map.terrains[terrains[i].name]=terrains[i];
}());
//-- utils
this.randTerrain=function()
{
var index=Math.floor(Math.random()*terrains.length-0.2);
return terrains[index>0?index:0];
}
this.drawFlag=function(x,y,color)
{
var x=x*this.cell_size+this.cell_size/2;
var y=y*this.cell_size+this.cell_size/2;
ctx.save();
ctx.fillStyle=color;
ctx.strokeStyle="#000";
ctx.beginPath();
ctx.arc(x,y,this.cell_size/3,0,2*Math.PI);
ctx.stroke();
ctx.fill();
ctx.restore();
}
//-- private classes
function Cell(x, y)
{
this.G="";
this.H="";
this.F=this.G+this.H;
this.x=x;
this.y=y;
this.list=0x0;
this.dad=0x0;
this.terrain=map.randTerrain();
this.drawDad=function(x,y)
{
ctx.save();
ctx.fillStyle="#4D92FF";
ctx.strokeStyle="#000";
ctx.beginPath();
ctx.arc(x,y,map.cell_size/10,0,2*Math.PI);
ctx.stroke();
ctx.fill();
ctx.restore();
}
this.render=function()
{
ctx.save();
ctx.fillStyle=this.terrain.color;
ctx.strokeStyle="#000";
ctx.fillRect(0,0,map.cell_size, map.cell_size);
ctx.strokeRect(0,0,map.cell_size, map.cell_size);
//Draw data
ctx.fillStyle="#000";
ctx.font = "10px Arial";
ctx.textAlign="start";
ctx.textBaseline="top";
ctx.fillText(this.F,1,1);
ctx.textBaseline="bottom";
ctx.fillText(this.G,1,map.cell_size);
ctx.textAlign="end";
ctx.fillText(this.H,map.cell_size-1,map.cell_size);
//Draw list
if(this.list)
{
ctx.strokeStyle=this.list=="open"?"#F00":"#a0F";
ctx.strokeRect(1,1,map.cell_size-2, map.cell_size-2);
}
//Draw dad
if(this.dad)
{
var offset=(map.cell_size/10)*3;
var x=offset;
var y=offset;
if(this.dad.x==this.x)
x=map.cell_size/2;
if(this.dad.x>this.x)
x=map.cell_size-offset;
if(this.dad.y==this.y)
y=map.cell_size/2;
if(this.dad.y>this.y)
y=map.cell_size-offset;
this.drawDad(x,y);
}
ctx.restore();
}
}
//-- constructor
for(var i=0;i<this.width;i++)
{
this.cells[i]=[];
for(var j=0;j<this.height;j++)
this.cells[i].push(new Cell(i,j));
}
//--methods
this.render=function()
{
for(var i=0;i<this.width;i++)
{
for(var j=0;j<this.height;j++)
{
ctx.save();
ctx.translate(i*this.cell_size,j*this.cell_size);
this.cells[i][j].render();
ctx.restore();
}
}
if(this.origin)
this.drawFlag(this.origin.x,this.origin.y,"#A65C3E");
if(this.destiny)
this.drawFlag(this.destiny.x,this.destiny.y,"#A92535");
}
this.fill=function(terrain, skip_render)
{
for(var i=0;i<this.width;i++)
for(var j=0;j<this.height;j++)
this.cells[i][j].terrain=terrain;
if(!skip_render)
this.render();
}
this.rect=function(terrain, x, y, w, h, skip_render)
{
for(var i=x;i<x+w;i++)
for(var j=y;j<y+h;j++)
this.cells[i][j].terrain=terrain;
if(!skip_render)
this.render();
}
this.addTerrain=function(terrain)
{
terrains.push(terrain);
indexTerrains();
}
this.getAdjacentCells=function(cell)
{
var adjacent_cells=[];
for(var i=cell.x-1;i<=cell.x+1;i++)
{
for(var j=cell.y-1;j<=cell.y+1;j++)
{
try
{
if(this.cells[i][j] && !(i==cell.x && j==cell.y))
adjacent_cells.push(this.cells[i][j]);
}
catch(ex) {}
}
}
return adjacent_cells;
}
}
function Pathfinding(map)
{
//OpenList class
function OpenList()
{
var cells=[];
this.add=function(cell)
{
cell.list="open";
cells.push(cell);
}
this.getFirst=function()
{
var first=cells.splice(0,1)[0];
return first;
}
this.sort=function()
{
cells.sort(function(a,b) {return a.F-b.F;});
}
this.contains=function(cell)
{
return cells.indexOf(cell)<0?false:true;
}
}
//ClosedList class
function ClosedList()
{
var cells=[];
this.add=function(cell)
{
cell.list="closed";
cells.push(cell);
}
this.contains=function(cell)
{
return cells.indexOf(cell)<0?false:true;
}
}
//init
var open_list=new OpenList();
var closed_list=new ClosedList();
var ctx=map.ctx;
open_list.add(map.cells[map.origin.x][map.origin.y]);
this.ended=false;
this.iterations=0;
//members
this.next=function(skip_render)
{
if(this.ended)
return;
this.interations++;
//get the first cell
var dad=open_list.getFirst();
closed_list.add(dad);
//add the adjacents cells to the open list
var adjacent_cells=map.getAdjacentCells(dad);
for(var i=0;i<adjacent_cells.length;i++)
{
var cell=adjacent_cells[i];
//~~~ Start check end
if(cell.x==map.destiny.x && cell.y==map.destiny.y)
{
this.ended=true;
cell.dad=dad;
if(!skip_render)
this.drawPath(cell);
return cell;
}
//~~~ End check end
//~~~ Start of the exclusion zone
if(!cell.terrain.awkwardness)
continue;
if(closed_list.contains(cell))
continue;
if(open_list.contains(cell))
{
var awk=cell.terrain.awkwardness;
//Change the dad and G,H,F if the current path is better
var newG=parseInt(cell.x!=dad.x && cell.y!=dad.y? dad.G+14/awk : dad.G+10/awk);
if(cell.G<newG) //worse? ok, skip
continue;
}
//~~~ End of the exclusion zone
one_change_at_least=true;
cell.dad=dad;
//Length to the origin
var awk=cell.terrain.awkwardness;
cell.G=Math.round(parseInt(cell.x!=dad.x && cell.y!=dad.y? dad.G+14/awk : dad.G+10/awk));
//Manhattan heuristic
var dx=Math.abs(map.destiny.x-cell.x);
var dy=Math.abs(map.destiny.y-cell.y);
cell.H=(dx+dy)*10;
//Update F
cell.F=cell.G+cell.H;
open_list.add(cell);
}
//sort open list
open_list.sort();
//render
if(!skip_render)
map.render();
}
this.drawPath=function(cell)
{
var offset=map.cell_size/2;
var next=cell.dad;
ctx.save();
while(next)
{
ctx.moveTo(cell.x*map.cell_size+offset,cell.y*map.cell_size+offset)
ctx.lineTo(next.x*map.cell_size+offset,next.y*map.cell_size+offset);
ctx.stroke();
cell=next;
next=cell.dad;
}
ctx.restore();
}
this.solve=function()
{
var last_cell=0x0;
while(!this.ended)
last_cell=this.next(true);
map.render();
this.drawPath(last_cell);
}
}
En estas 300 líneas (me ha llevado media mañana escribirlas!) tenéis todo lo necesario para crear mapas y resolver caminos. Un ejemplo de ejecución (el que crea el último mapa grande que hemos visto) sería:
var map=new Map(30,15,50,canvas);
map.fill(map.terrains.ground)
map.rect(map.terrains.wall, 4, 2, 2, 6);
map.rect(map.terrains.water, 8, 0, 4, 15);
map.rect(map.terrains.deep_water, 9, 0, 2, 15);
map.rect(map.terrains.forest, 13, 6, 5, 5);
map.rect(map.terrains.water, 15, 1, 4, 4);
map.rect(map.terrains.deep_water, 16, 2, 2, 2);
map.rect(map.terrains.wall, 19, 3, 1, 6);
map.rect(map.terrains.bridge, 8, 10, 4, 1);
map.origin={x:2,y:2};
map.destiny={x:27,y:4};
map.render();
var pathfinding=new Pathfinding(map);
//Para avanzar un paso pathfinding.next();
//Para resolver directamente pathfinding.solve();
He de decir que he disfrutado mucho escribiendo este pequeño código. Mi parte favorita son las líneas de las 26 a las 31. ¿Todo el mundo las entiende y sabe qué hacen y por qué funcionan? 😉
Leer másConjunto de Mandelbrot
Dejo un pequeña “piece of code” de hace un par de años para generar el conjunto de Mandelbrot en un canvas con Javascript. Quería tener una imagen muy grande del conjunto con tonos azules, así que decidí generarla de la forma más rápida posible: un canvas y unas pocas líneas de código.
Fue una mala idea, descubrí entonces que la mayoría de navegadores soportan como máximo una dimensión en píxeles de 8192×8192 para el canvas; así que la imagen se limitaría como mucho a ese tamaño.

Descargar imagen final en tamaño completo
En cualquier caso… desde aquí podéis ejecutar el script; y el código (hecho ad hoc para generar la imagen y nada más):
var width=7500;
var height=width*0.88;
var canvas=document.getElementById("canvas");
var control=document.getElementById("control");
canvas.width=width;
canvas.height=height;
var context=canvas.getContext("2d");
var minAbsRe=-2.00;
var maxAbsRe=+0.80;
var minAbsIm=-1.25;
var maxAbsIm=+1.25;
var zoom=1;
var y=0;
function draw()
{
var minRe=minAbsRe*zoom;
var maxRe=maxAbsRe*zoom;
var minIm=minAbsIm*zoom;
var maxIm=maxAbsIm*zoom;
var reFactor=(maxRe-minRe)/(width-1);
var imFactor=(maxIm-minIm)/(height-1);
var maxIterations = 30;
var c_im=maxIm-y*imFactor;
for(var x=0;x<width;++x)
{
var c_re=minRe+x*reFactor;
var zRe=c_re, zIm=c_im;
var isInside=true;
for(var n=0;n<maxIterations;++n)
{
var zRe2=zRe*zRe,zIm2=zIm*zIm;
if(zRe2+zIm2>4)
{
isInside=false;
if(n<maxIterations/2)
context.fillStyle="rgb(0,0,"+(n*255/(maxIterations/2))+")";
else
{
var a=Math.round((n-(maxIterations*0.5))*255/(maxIterations/2));
var b=Math.round(a*Math.pow(n/maxIterations,3));
context.fillStyle ="rgb("+b+","+a+",255)";
}
context.fillRect(x,y,1,1);
break;
}
zIm=2*zRe*zIm+c_im;
zRe=zRe2-zIm2+c_re;
}
if(isInside)
{
context.fillStyle="#000";
context.fillRect(x,y,1,1);
}
}
if(y<height)
{
var progress=(y*100/height);
control.innerHTML=progress.toFixed(2)+"%";
y++;
setTimeout(draw,25);
}
else
{
var img=canvas.toDataURL("image/png");
control.innerHTML='<img src="'+img+'"/>';
}
}
Leer más